
ARCHEOASTRONOMIA LIGUSTICA
Pubblicato in: Atti del XV Seminario A.L.S.S.A. di Archeoastronomia, Genova,
13-14 aprile 2013, pp. 152-170.
il Metodo
Nautico
per il calcolo dell�azimut di
un allineamento e della declinazione da esso sottesa
Mario
Codeb�
Agostino Frosini
Descrizione (di Mario Codeb�)[1]
Vengono qui di seguito date, con esempi
numerici, due fondamentali sequenze di formule che consentono di determinare
l�azimut astronomico A di un allineamento e la declinazione δ sottesa, essendo noti:
1) le coordinate geografiche latitudine
φ, longitudine λ,
quota sul livello del mare �e�[2];
2) l�angolo α tra l�allineamento e l�astro (generalmente il Sole),
misurato con il teodolite o con lo squadro sferico graduato, nell�istante della
misurazione.
Le due sequenze sono valide per
misurazioni prese col Sole, ma possono essere utilizzate anche con Luna, stelle
e pianeti apportando alcune modifiche (che qui non vengono descritte).
I valori tabulari si desumono dalle
Effemeridi in corso. Nell�esempio che segue sono state utilizzate quelle
nautiche pubblicate dall�Istituto Idrografico della Marina Militare Italiana
I.I.M., dette Effemeridi Nautiche (EN) o Almanacco Nautico (in inglese: Nautical
Almanac NA). Perci� le sigle usate sono quelle proprie di tale almanacco[3].
Le procedure di calcolo sono desunte da
Flora 1987 ed adattate alle necessit� dell�archeoastronomia.
Le correzioni da apportare al barometro
a mercurio sono descritte nella tavola XIII del volume Tavole Nautiche dell�I.I.M., mentre i valori della rifrazione
atmosferica nella tavola XXII.
Le abbreviazioni, i simboli e le sigle
usate sono le seguenti:
� = Sole;
� = Luna;
� = stella;
● = pianeta;
h,
m, s = ore, minuti e secondi di tempo;
sen
= seno;
cos
= coseno;
tan
= tangente;
*
= moltiplicazione;
tm
= tempo medio del luogo di osservazione, ovvero sua ora civile (la comune ora segnata
dall�orologio);
Tm
= tempo medio di Greenwich, ovvero sua ora civile (altrimenti detto UT e, con
dizione scorretta, GMT[4]);
tv
= tempo vero, ossia angolo orario del centro dell�astro contato a partire dal
meridiano superiore dell�osservatore verso W. Il meridiano superiore � quel
meridiano che comprende un polo dell�equatore e lo zenit dell�osservatore. Il
meridiano inferiore � quello che contiene l�altro polo dell�equatore ed il
nadir dell�osservatore;
Tv
= il tempo vero al meridiano di Greenwich;
H
= angolo orario, ossia tv, dell�astro;
A
= azimut;
Am
= azimut misurato con lo strumento (teodolite o squadro sferico graduato);
Aa
= azimut dell�allineamento;
φ =
latitudine;
λ =
longitudine;
δ =
declinazione;
ET
= equazione del tempo, ossia differenza algebrica tra il tempo vero ed il
simultaneo tempo medio (o viceversa, con relativo cambiamento di segno
algebrico): ETm = tv � tm (equazione del tempo medio) oppure: ETv
= tm � tv (equazione del tempo vero);
JD
= giorno giuliano;
hv
= altezza vera dell�astro;
ho
= altezza misurata (altrimenti detta osservata) dell�astro;
R
= rifrazione atmosferica;
Q
= altezza sul livello del mare dell�occhio dell�osservatore, comprensiva di
quota sul livello del mare e di altezza dal suolo dell�occhio dell�osservatore;
i
= depressione dell�orizzonte; per calcolarla qui � usata la formula: i = 0,03 √Q;
Π:
parallasse. Quella del Sole Π� vale, al 2000.0, mediamente 0�00�08,794148�. Quella
della Luna Π� vale mediamente 0�57�02,7� quando essa �
all�orizzonte astronomico e (0�57�02,7�cos ho) quando invece � sopra di esso di
una quantit� �ho� (misurabile con il cerchio zenitale del teodolite, o con
l�inclinometro o con il sestante). Quella delle stelle Π� � evanescente. La parallasse di Sole, Luna e pianeti Π● pu� anche essere ricavata dalla tavola XXIV
delle Tavole Nautiche. Nelle Effemeridi Nautiche quella lunare � data di ora in
ora per ciascun giorno dell�anno;
Sd
= semidiametro di un astro. Vale praticamente solo per Sole e Luna, che si
presentano visivamente come dischi. Nelle Effemeridi Nautiche � dato
giornalmente per
z
= distanza zenitale. E� l�inverso dell�altezza; perci� vale z = 90� � h;
ε =
obliquit� (angolare) dell�eclittica;
Pmb
= pressione atmosferica in millibars;
PmmHg
= pressione atmosferica in millimetri di mercurio. Le relazioni che legano tra
loro queste due ultime grandezze sono le seguenti: Pmb = PmmHg 3/4; PmmHg = Pmb
4/3;
Im
= intervallo medio nelle EN;
Iv
= intervallo vero nelle EN;
pp
= parti proporzionali nelle EN;
d
= differenza oraria della declinazione (con il suo segno) nelle EN.
Questi
ultimi quattro segni sono adottati nelle Effemeridi Nautiche per le interpolazioni
con le apposite tabelle annesse (nelle pagine colorate).
a) Si trasforma il tm in Tm sottraendo o aggiungendo
al tm l�ora del fuso orario locale a seconda, rispettivamente, se questo � a E
o a W di Greenwich:
Tm = tm � ora del fuso
orario locale (� se ad E di Greenwich; + se ad W).
b)
Trasformato il tm in Tm, si trascurano momentaneamente i minuti ed i secondi
(che in questa circostanza prendono il nome di Im1) e per il solo
valore delle ore si cerca nella colonna T delle EN il corrispondente valore
espresso in gradi sessagesimali: questo � il Tv della sola ora. Nelle pagine
colorate delle EN si cerca quello corrispondente ai minuti di Im e nella
colonna secondi, in corrispondenza ai secondi di Im, si trova, nella colonna
intestata �Sole e pianeti� (se si stanno utilizzando questi nella misurazione.
Se invece si sta utilizzando
c) Al Tv di ore, minuti e secondi si somma la
longitudine λ del sito con il suo segno: in astronomia nautica la
longitudine si considera positiva ad E e negativa ad W[5]. Si
ottiene cos� il tv:
tv
= Tv � λ.
Nell�effettuare
questi calcoli conviene innanzitutto trasformare tutti i valori orari o
sessagesimali nei corrispettivi valori decimali. Per far ci� si dividono i
secondi (sia di tempo che di grado) per 60 e si ottengono parti decimali di
primo; poi si dividono i primi e le parti decimali gi� ottenute per 60 e si
ottengono parti decimali di ore o di gradi. Le calcolatrici eseguono questa
trasformazione oppure hanno un apposito tasto.
Es.
1: convertire 20�12�47� in parti decimali:
47�/60
= 0,78(3)[6]
12,78(3)�/60
= 0,2130(5)
risultato:
20,2130(5)�
Es.
2: convertire in parti decimali l�orario 4h56m37s (4 ore, 56 minuti, 37
secondi):
37/60
= 0,61(6)
56,61(6)/60
= 0,9436(1)
risultato:
ore 4,9436(1)
Per
trasformare i valori decimali in sessagesimali od orari si procede come sopra,
ma moltiplicando per 60.
Es.
3: convertire 20,2130(5)� in gradi sessagesimali:
0,2130(5)�
* 60 = 12,78(3)�
0,78(3)�
* 60 = 46,(9)�
risultato:
20�12�47�
Es.
4: convertire l�orario 4,9436(1) ore in ore, minuti e secondi:
0,9436(1)
* 60 = 56,61(6) minuti
0,61(6)
* 60 = 36,(9) secondi
risultato:
4h56m37s.
Inoltre
se le coordinate sono date in valori differenti (in genere la longitudine in
valori orari e la latitudine in valori sessagesimali) occorre necessariamente
trasformarle in un�unica unit� di misura, oraria o sessagesimale, e poi
decimale. Di solito conviene di pi� trasformare le coordinate orarie in
sessagesimali. Per far ci� basta moltiplicare il valore orario decimale per 15.
All�opposto, per trasformare i valori sessagesimali decimali in orari basta
dividerli per 15.
Es.
5: trasformare l�orario 4h56m37s in gradi sessagesimali:
4h56m37s
= 4,9436(1); 0,9436(1) * 15 = 4,1541666667� = 74�09�15�
Es.
6: trasformare 74�09�15� in ore, minuti e secondi:
74�09�15�
= 74,1541666667 / 15 = 4,9436(1) = 4h56m37s.
Si
rammenti che le calcolatrici scientifiche trasformano automaticamente i valori
orari e sessagesimali in decimali, perch� internamente eseguono i calcoli
sempre con tale formato.
d)
Si calcola ora la declinazione δ. Nelle EN di fronte al valore T (cio� a
Tv) nella colonna intestata Dec. si trova il valore della declinazione oraria
δ, che pu� essere S o N. Il solo valore dei minuti, arrotondato dei
secondi per difetto, costituisce l�Im dei minuti arrotondati per difetto. In
fondo alla colonna, a pie� di pagina, si trova la sigla �d� seguita da un
valore numerico molto basso preceduto dal segno algebrico �; per il Sole esso
oscilla tra d +1.0 e d �1.0. Nella pagina colorata corrispondente al valore di
Im arrotondato per difetto, nelle colonne �v/d� si cerca il valore numerico di
�d�: di fronte ad esso, nella colonna �pp� (parti proporzionali) si trova un
valore in primi e decimi di primo sessagesimali. Il valore �pp� si somma
algebricamente con il segno di �d� a δ dell�unit� oraria. Si considera ora
il solo valore dei minuti arrotondato per eccesso dell�importo dei secondi
(ossia un minuto in pi� del valore di Im) o Im arrotondato per eccesso. Nella
pagina colorata del suo valore si cerca nella colonna �v/d� il corrispondente
valore di �pp�; se esso � uguale a quello trovato per Im arrotondato
per difetto lo si trascura; se � diverso si fa la media tra i due valori (o,
meglio, s�interpola) ed il risultato si somma a δ dell�unit� oraria con il segno di �d�. Si ottiene cos�
la declinazione δ dell�astro in quel preciso
momento di Tm, completo di ore, minuti e secondi. Anche in questo caso, come
gi� per il Tv di cui al punto b), si � eseguita in modo semplice
un�interpolazione[7].
e) Ora si calcola l�altezza �h� dell�astro con la
formula[8]:
sen h = sen δ * sen φ + cos δ * cos φ * cos tv.
f) Si calcola l�azimut A dell�astro:
cos A = (sen δ � sen φ * sen h) / (cos φ cos h).
Si
ricava A con le tavole delle funzioni trigonometriche o con la funzione
arcocoseno. Se il tv (di cui al punto c) � <180� allora A � quello trovato
con la formula sopra indicata; se invece il tv � >180� allora
As
= 360� � A.
g)
Si calcola l�azimut Aa dell�allineamento aggiungendo o sottraendo all�azimut A
l�angolo α misurato con il teodolite o con lo squadro sferico:
Aa = A � α. E precisamente: si aggiunge l�angolo α se l�astro deve ancora passare sull�allineamento
misurato e invece lo si sottrae se � gi� passato su di esso.
h)
A questo punto si deve calcolare l�altezza vera �hv� dell�astro rispetto alla
�ho� misurata con il cerchio zenitale del teodolite o con l�inclinometro.
Infatti l�altezza vera �hv� differisce da quella misurata per un considerevole
numero di parametri: la rifrazione, la depressione dell�orizzonte, il
semidiametro[9], la parallasse.
h1)
La rifrazione R � il fattore pi� importante e costituisce uno dei capitoli pi� complessi
dell�astronomia sferica poich� essa dipende dalle condizioni fisiche �
temperatura, pressione, umidit�, ecc. � di tutti gli strati d�aria che
il raggio di luce attraversa dalla stratosfera fino al suolo, trasformandosi da
raggio incidente in raggio rifratto. Quest�ultimo pone l�immagine visiva
dell�astro ad un�altezza sempre maggiore di quanto esso si trovi fisicamente
nella realt� (per es. all�alba l�immagine del Sole sull�orizzonte astronomico �
gi� visibile alcuni minuti prima del suo effettivo sorgere ed al tramonto �
ancora visibile per alcuni minuti dopo che � effettivamente tramontato). La
rifrazione � nulla allo zenit e massima all�orizzonte astronomico: diminuisce,
quindi, con l�aumentare dell�altezza �h� sull�orizzonte astronomico o � che �
lo stesso � con il diminuire della distanza zenitale �z�[10]. Per
altezze di astri >15� (ossia per distanze zenitali z < 85�) sono
disponibili numerose formule, ma per altezze inferiori a 15� (ossia distanze
zenitali z > 85�) solo la formula di Bennet (Meeus 2005, pp. 105 � 108)[11] d�
risultati attendibili[12],
oppure occorre utilizzare apposite tabelle, costruite sulla base di
osservazioni empiriche. Esse sono generalmente allegate alle principali
effemeridi (Conaissance de Temps, American Nautical Almanac, ecc.), ma non a
quelle dell�I.I.M. che le pubblica invece nelle sue Tavole Nautiche alla tavola
n. XXII, nella quale al valore della rifrazione media occorre apportare le due
correzioni per la temperatura prima e per la pressione barometrica poi,
entrambe misurate nel luogo di osservazione. Per un�esauriente discussione del
problema della rifrazione atmosferica si veda in AA.VV. 1976 � 1987, vol. III
parte I, pp. 514 � 516; Flora 1987, pp. 285 � 315; Lenzi 1967, pp. 24 � 26;
Meeus 2005, pp. 105 � 108; Smart 1977, pp. 58 � 73; Zagar 1984, pp. 205 � 226.
h2)
La depressione dell�orizzonte �i� � data dalla formula
i
= 0,03 * √Q
dove
�Q� � l�altezza in metri sul livello del mare dell�occhio dell�osservatore,
comprensiva cio� della quota in metri del luogo sul livello del mare e
dell�altezza in metri dell�occhio dell�osservatore dal suolo. Per
approfondimenti sulla teoria della depressione dell�orizzonte si veda Flora
1987, pp. 285 � 315.
Si
badi bene che la formula per il calcolo di �ho� non si riferisce pi� all�astro
che abbiamo test� misurato con il teodolite ed il cronometro astronomico, ma
all�astro incognito verso il quale reputiamo che il monumento archeologico sia
orientato. Se supponiamo che esso sia diretto verso una stella e comunque per
una prima approssimazione, questi tre parametri �ho�, �i� ed �R� sono
sufficienti.
Se
il calcolo eseguito ci fa supporre trattarsi di un pianeta visibile ad occhio
nudo occorre aggiungere anche la parallasse Π● secondo la tavola
XXIV delle Tavole Nautiche. Se, infine, abbiamo ragione di credere trattarsi
del Sole o della Luna occorre introdurre nella formula anche i valori di
parallasse Π� e Π� e semidiametro Sd� ed Sd�: questi due astri, infatti, non appaiono puntiformi come
le stelle e i pianeti, ma presentano entrambi l�immagine di un disco che ha
un�ampiezza di circa mezzo grado. La parallasse va aggiunta nella formula.
Quella del Sole � molto piccola, essendo il suo valore 0�00�08,794148� ed �
pressoch� costante, data la sua grande distanza dalla Terra. Quella della Luna
� maggiore, ma soprattutto varia di ora in ora a seconda dell�altezza del
satellite sull�orizzonte astronomico ed � data di ora in ora per ogni giorno
dell�anno dall�apposita colonna PAR delle EN. In alternativa si pu� usare il
valore medio Π� = 0�57�02,7� (parallasse orizzontale media), ma
introducendo cos� un errore. Se invece il satellite ha una qualche altezza ho≠0�00�00�
il valore della sua parallasse � dato, in prima approssimazione, dalla formula:
Π� * cos ho.
Attenzione!
Le EN danno la parallasse Lunare di ora in ora per ogni giorno dell�anno, ma
questi valori servono solo nel caso che
h3)
Il semidiametro �Sd� o raggio angolare � la met� della misura apparente del
disco visibile del Sole e della Luna. Esso varia in funzione diretta della
distanza della Terra dai due astri, perci� quello del Sole varia in un ciclo di
365 giorni, mentre quello della Luna in un mese sinodico. La tavola XXIII delle
Tavole Nautiche consente di calcolarlo in funzione dell�altezza apparente o
istrumentale (equivalente alla nostra ho) misurata con il sestante, alla quale
vanno apportate le correzioni d�indice e istrumentale. Le EN riportano
direttamente giorno per giorno i valori del semidiametro lunare e solare; ma,
come detto per la parallasse e per la medesima ragione, conviene inserire nella
formula dell�altezza vera il semidiametro medio. Questo � per il Sole
mediamente 0�16�01� e per
In
definitiva le formule archeoastronomiche per trasformare l�altezza misurata
�ho� in altezza vera �hv� con sufficiente precisione sono le seguenti:
h4) valida per le stelle ed in prima approssimazione:
hv = ho � (0,03 * √Q)
� R
h5) valida per i pianeti:
hv
= ho � (0,03 * √Q) � R + (Π● * cos ho)
h6) valida per Sole e Luna:
hv
= ho � (0,03 * √Q) � R � Sd + (Π� o Π� * cos ho).
Esse
vanno eseguite esattamente nella sequenza indicata, a differenza di quanto
descritto erroneamente in precedenza (Codeb� 1997).
Esistono
altre due formule per la correzione delle altezze misurate: quella geodetica e
quella nautica (Codeb� 2010). Sono pi� precise perch� trasformano la parallasse
orizzontale equatoriale in parallasse locale in altezza, correggendo �ho� anche
in funzione della latitudine dell�osservatore, ma sono anche pi� complicate. A
causa di ci� si sbagliano facilmente calcolandole con le tavole trigonometriche
e con la calcolatrice, cio� �a mano�. Devono quindi essere riservate
all�esecuzione di un programma scritto e testato, come il programma metodo nautico scritto da Agostino
Frosini in linguaggio Java Script nel quale l�operatore ha la possibilit� di
scegliere tra la formula semplificata, quella geodetica e quella nautica.
Queste ultime due differiscono l�una dall�altra nel risultato per soli decimali
di secondi sessagesimali: sono quindi interscambiabili. La formula semplificata
differisce invece dalle altre due per i secondi sessagesimali, ma la sua
semplicit� � e quindi la minore probabilit� di sbagliarla � ne fanno la formula
d�elezione nei calcoli �a mano�.
i)
Infine si calcola la declinazione �δ� dell�astro sconosciuto:
sen δ = sen φ * sen hv + cos φ * cos hv * cos A
se
si conta l�azimut da N;
sen δ = sen φ * sen hv � cos φ * cos hv * cos A
se
si conta l�azimut da S;
sen δ = sen φ * cos z + cos φ * cos z * cos A
se
si utilizza la distanza zenitale �z� contando l�azimut A da N;
sen δ = sen φ * cos z � cos φ * cos z * cos A
se
si utilizza la distanza zenitale �z� contando l�azimut A da S;
e
con le tavole trigonometriche o con la funzione arcoseno si ricava δ.
Dal
valore numerico della declinazione e dal suo segno algebrico si deduce di quale
astro si tratta. Qui di seguito sono dati i valori (pressoch� uguali sia per
l�alba che per il tramonto) che furono maggiormente oggetto di indagine
nell�antichit�:
a)
Sole al J2000.0
21/03
(equinozio di primavera): δ 0�
21/06
(solstizio d�estate): δ +23�26�21,448�
23/09
(equinozio d�autunno): δ 0�
21/12
(solstizio d�inverno): δ �23�26�21,448�.
Nell�emisfero boreale il segno
algebrico sar�, ovviamente, + per la declinazione settentrionale (ossia estiva)
e � per quella meridionale (ossia invernale). L�inverso in quello australe.
Per
Per quanto riguarda le stelle, la loro
declinazione � propria per ciascuna e varia lentamente nel tempo per effetto
della precessione degli equinozi e del moto proprio di ogni stella (Codeb�
2011; 2012).
Per quanto invece riguarda i pianeti
visibili ad occhio nudo � i soli che interessano l�archeoastronomia � il loro
moto � ciclico e tende a diventare caotico col passare dei millenni. Essi
comunque giacciono sull�eclittica. La teoria planetaria � troppo complessa per
essere descritta qui. I lettori interessati possono leggerla in Meeus 1988 e
1990, capp. 22 � 25; 2005, capp. 30 � 33 e appendice III e in vari capitoli[13] dei
cinque volumi Mathematical Astronomy
Morsels di Jean Meeus. In ogni caso, i calcoli pi� precisi circa il moto e
le posizioni dei pianeti sono oggi facilmente ottenibili col software gratuito
Solex 11.0 del dott. Aldo Vitagliano che utilizza l�integrazione numerica,
probabilmente pi� precisa, nei lunghi periodi di tempo tipici
dell�archeoastronomia, della teoria VSOP87[14] di
Bretagnon e Francou (Meeus 2005, pp. 217 � 221).
Le declinazioni odierne del Sole e
della Luna si possono trasformare in quelle all�epoca della costruzione del
monumento con la formula di Laskar, che � sufficientemente precisa fino a 10000
anni dal 2000 d. C.[15]:
U = T / 100
δantica = δ�hh, mm, ss + δ� � 1�18�00,93� * (U) � 0�00�01,55� * (U)� + 0�33�19,25� * (U)� �
0�00�51,38� + (U)4 � 0�04�09,67� * (U)5 � 0�00�39,05� *
(U)6 + 0�00�07,12� * (U)7 + 0�00�27,87� * (U)8
+ 0�00�05,79� * (U)9 + 0�00�02,45� * (U)10
Esempi
numerici (di Mario Codeb�)[16]
Esempio I)
L�esempio numerico che segue � relativo
al dolmen di Borgio Verezzi (SV) sul M. Caprazoppa (Codeb� 1997a, pp. 735 �
751).
Nelle misurazioni sul terreno
dell�epoca, nell�impossibilit� di misurare l�azimut dell�asse medio perch� non
identificabile a causa dello stato di conservazione del megalite, fu necessario
misurare l�angolo α tra entrambi i lati esterni
della costruzione ed il Sole. Ci� fu reso possibile in una sola battuta (ossia
con una sola misurazione angolare) grazie ad una procedura (il cui algoritmo
sintetico � riportato in Codeb� 1997a, p. 737) appositamente elaborata da Mario
Monaco, segretario dell�Associazione Astrofili Savonesi, che collabor� alla
campagna di rilevamento.
I dati iniziali furono:
giorno dell�osservazione: 26/12/1994
ora civile locale tm: 12h53m35s
φ: 44�10�23�N
λ: 8�18�52�E
e: m. 302,5 s.l.m.
angolo α1:
57�09�40�
angolo
α2: 48�45�39�
01)
Tm (12h53m35s � 01h00m00s) = 11h53m35s
02)[17]
|
Tm
11h00m00s del 26/12/1994: |
Tv�� 344�52,7�+ |
|
Im
00h53m35s |
Iv��� 013�23,8�+ |
|
ν
�0,2 |
pp� �000�00,2�= |
|
Tv� 11h53m35s del 26/12/1994 |
����� 358�16�18� |
03)
|
Tv� |
����� 358�16�18� + |
|
φ |
����� 008�18�52�E = |
|
tv� |
����� 366�35�10�� � |
|
riduzione
al I quadrante |
����� 360�00�00� |
|
tv� |
����� 006�35�10� |
04)[18]
|
δ� 26/12/1994 Tm 11h00m00s |
S� ���23�21,8�+ |
|
Im 00h53m00s d +0,1 |
pp���� 00�00,1�= |
|
δ� 26/12/1994 Tm
11h53m |
����� �23�21�42� |
|
δ� 26/12/1994 Tm
11h00m00s |
S���� �23�21,8�+ |
|
Im 00h54m00s d +0,1 |
pp���� 00�00,1�= |
|
δ� 26/12/1994 Tm
11h54m |
����� �23�21�42� |
quindi[19]:
δ� 26/12/1996 Tm
11h53m35s = �23�21�42�
05)
sen h� = sen �23�21�42� * sen 44�10�22� +
cos �23�21�42� * cos 44�10�22� * cos 6�35�10�
h� = 22�11�47,04�
06) cos A� = (sen �23�21�42�
� sen 44�10�22� *
sen 22�11�47,04�) / (cos 44�10�22� * cos 22�11�47,04�)
07) poich� �tv� < 180�, allora:
A� = 360� � 173�28�12,5� = 186�31�47,5�
08) Aallineamento1 = 186�31�47,5� �
57�09�40� = 129�22�07,5�
09)[20] hv� = 0� � [0,03 * √(302,5 + 1,65)] � 0�36�29� =
�1�07�52,51�
10) sen δallineamento1 hv� = sen 44�10�22� * sen �1�07�52,51� +
cos 44�10�22� *
cos �1�07�52,51� * cos 129�22�07,5�
δallineamento1
hv� = �27�56�41,46�
11) poich� δallineamento1
hv� ha un valore compreso tra la minima declinazione
solare �23�26�21,448� J2000.0[21],
quale si verifica al solstizio d�inverno, e la minima declinazione lunare
�28�35�21,45� � 0�09�, quale si verifica ogni 6798 giorni al lunistizio minimo[22], si
pu� supporre che l�asse di questo monumento sia orientato sul sorgere della
Luna. Occorre quindi ripetere il calcolo di �hv� e di �δ� per i valori lunari corretti di semidiametro e
parallasse orizzontale medi:
hv� = 0� � [0,03 * √(302,5
+ 1,65)][23] � 0�36�29� + 0�16�[24] + (0�57�02,7� *
cos 0�)
hv� = 0�05�10,19�[25]
12) sen δallineamento1 hv� = sen 44�10�22� * sen 0�05�10,19� + cos
44�10�22� * cos 0�05�10,19� * cos 129�22�07,5�
δallineamento1 hv� = �26�59�40,08�
Dunque l�azimut 129�22�07,5�, calcolato a partire da
un angolo misurato col Sole in data 26/12/1994, ora civile locale tm 12h53m35s,
con altezza misurata di orizzonte 0�00�00�, corrispondente all�orizzonte
marino, sottende una declinazione δ1 = �26�59�40,08�, molto prossima alla declinazione
lunare al lunistizio minimo �28�35�21,45� � 0�09�.
Esempio II)
L�identico calcolo dell�azimut del secondo angolo α2:
48�45�39� d� come risultato finale una declinazione sottesa δ2 =
�32�00�26,2�, quindi la declinazione media sottesa dal dolmen � δμ = �29�30�03,14� σ � 2,5�. I lettori provino ad eseguire il calcolo da
soli.
Esempio III)
Il giorno 24/06/2013, in localit� φ 43�56�21�N e λ
7�57�05,1�E, alle ore tm 14h59m27s, con lo squadro sferico graduato e la
livelletta Abney, sono stati misurati un angolo col Sole α 148,90g = 134�00�36� ed un�altezza ho =
21�20�. Calcolare la declinazione sottesa.
tm 14h00m00s = Tm 12h00m00s = Tv�� 359�23,3� +
Im 00h59m27s������������ = Iv��
014�51,8� +
ν �0,1������������������������� = pp� �000�00,1� =
�����������������������������������������
Tv�������������������������������� =����� 374�15�00� �
riduzione al I quadrante���� =��
360�00�00� =
�����������������������������������������
Tv������������������������������ =����� 014�15�00,0� +
������������������������������� =�������� 007�57�05,1� =
�������������������������������������������
tv���������������������������������� =����� 022�12�05,1�
δ� UT 12h00m00s�� =���
+23�23,9� +
Im 00h59m00s d 0,0
= pp� 00�00,0� =
���������������������������������
δ� UT 12h00m00s���� =����
23�23,9�
Poich� per� δ� UT 13h00m00s = 23�23,8� occorre interpolare:
δ� UT 13h00m00s������ =���
+23�23,8� +
Im 00h59m00s d
0,0��� = pp�� 00�00,0� =
���������������������������������
δ� UT 13h00m00s������ =�����
23�23,8�
δ� 23�23,9� � δ� 23�23,8� = 0�00,1�
Si trasformano le unit� di tempo in gradi
sessagesimali moltiplicandole per 15:
UT 13h00m00s � UT
12h00m00s = 1h = 15�
1h00m00s � 0h59m27s = 0h00m33s * 15 = 0�08�15�
E si riducono tutti i valori alla medesima unit�: i
secondi sessagesimali:
15� =
0�00,1� = 0�00�06�
Ora si effettua una proporzione:
X� = (0�00��6� * 0�08�15�) /
Si sottrae X� da δ� UT 13h00m00s:
23�23,8� �
0�00�00,06� = 23�23�47,94�
Quindi δ� UT 12h59m27s =
23�23�47,94�
Naturalmente, essendo la differenza tra UT 12h59m27s e
UT 13h00m00s di soli 33s, si poteva assumere per δ� UT 12h59m27s lo
stesso valore di δ� UT 13h00m00s senza apprezzabile errore. Diverso
sarebbe stato il caso in cui la differenza di orario fosse stata per esempio di
mezz�ora = 7�30�: in caso di medie e forti differenze di tempo l�interpolazione
diventa obbligatoria.
Ora si calcola l�altezza del Sole h� nell�istante della misurazione:
sen h� = sen 23�23�47,94�
* sen 43�56�21,2� +
cos 23�23�47,94� * cos 43�56�21,2� * cos 22�12�05,1�
h� = 62�33�00,98�
Ora si calcola l�azimut del Sole nell�istante della
misurazione:
cos A�1 = (sen
23�23�47,94� � sen 43�56�21,2� * sen 62�33�00,98�) / (cos 43�56�21,2� * cos
62�33�00,98�)
A�1 =
131�12�31,19�
Poich� tv < 180�, allora A� = 360� � A�1:
A� = 360� � 131�12�31,19� = 228�47�28,81�
Al valore di A� si aggiunge
algebricamente il valore di α per ottenere
l�azimut esatto dell�allineamento. In questo caso, poich� il Sole era gi�
transitato sull�allineamento, α va
sottratto:
Aa = 228�47�28,81� � 134�00�36� = 94�46�52,81�
Ora si calcola l�altezza vera hv�
hv� = 21�20� � 0,03 * √(436 + 1,65) � 0�02�28� =
20�39�52,63�
e la relativa declinazione sottesa:
sen δallineamento hv� = (sen 43�56�21,2�
* sen
20�39�52,63� + cos 43�56�21,2� * cos 20�39�52,63� * cos 94�46�52,81�)
δallineamento hv� = 10�52�39,97�
Poich� questo valore � uno di quelli assunti dal Sole
nel corso dell�anno ed � invece inferiore a quelli minimi assunti dalla Luna
(�18�18�), si ripete il calcolo con hv�:
hv� = 21�20� � 0,03 * √(436 + 1,65) � 0�02�28� +
0�15,7� + (0�00�08,794148� * cos 21�20�) = 20�55�42,82�
sen δallineamento hv� = sen 43�56�21,2� * sen 20�55�42,82�
+ cos
43�56�21,2� * cos 20�55�42,82� * cos 94�46�52,81�
δallineamento hv� = 11�03�28,44� (declinazione assunta dal Sole alle
date 18/04 e 24/08/ 2013).
Algoritmo sintetico (di Mario Codeb�)
1) calcolo dell�angolo orario
locale del Sole o tv
tm � fuso orario locale E o +
fuso orario locale W = Tm
Tm h:��������� Tv� h +
Im mm e ss: Iv���� +
�ν:������������ �pp��� =
�����������������������
��������� TV� hh, mm, ss
Tv� hh, mm, ss +
+ λ E; � λ W��� =
����������������
tv�
2) calcolo della declinazione
del Sole
δ�hh���������������������� +
Im mm inferiori �d� =
������������������
δ�hh, mm inferiori
δ�hh����������������������� +
Im mm superiori �d� =
�������������������
δ�hh, mm superiori
δ�hh, mm, ss = interpolazione tra δ�hh mm inferiori e δ�hh mm superiori
3) calcolo dell�altezza
geometrica dell�astro
sen h� = sen δ� sen φ + cos δ� cos φ cos tv
4) calcolo dell�azimut del
Sole (contato da Nord)
cos A� = (sen δ� � sen φ sen h�) / (cos φ cos
h�)
se tv > 180�, allora A�1 = A�
se tv < 180�, allora A�1 = 360� �
A�
5) calcolo dell�allineamento
del monumento
Aa = A�1 � Am
6) riduzione di ho
in hv
hv� e � = ho � 0,03�Q � R �Sd + (Π cos
ho)
hv● = ho � 0,03�Q � R + (Π● * cos
ho)
hv� = ho � 0,03�Q � R
7) calcolo della declinazione
sottesa al momento della misurazione (da N)
sen δ = sen φ sen hv + cos φ cos hv cos Aa
8) eventuale riduzione della
declinazione all�epoca della costruzione del monumento (formula di Laskar)
{[(JD � 2451545,0) / 36525] /
100} = U
δ�hh, mm, ss + δ� � 1�18�00,93� * (U) � 0�00�01,55� * (U)� +
0�33�19,25� * (U)� � 0�00�51,38� + (U)4 � 0�04�09,67� * (U)5
� 0�00�39,05� * (U)6 + 0�00�07,12� * (U)7 + 0�00�27,87� *
(U)8 + 0�00�05,79� * (U)9 + 0�00�02,45� * (U)10
Presentazione del software di calcolo il Metodo
Nautico (di
Agostino Frosini)
Questo
programma calcola la declinazione sottesa dall�azimut di un monumento
utilizzando le Effemeridi Nautiche dell�I.I.M. per il calcolo dell�azimut del Sole
in un preciso istante UT.
Il
Software, assieme ad altri � oggi pubblicato sul sito:
http://www.archaeoastronomy.it/nostre_ricerche.htm
Potrete
utilizzarlo online oppure scaricarlo gratuitamente ed eseguirlo sul vostro PC.
L�elaborato
� stato scritto in linguaggio Javascript perch� compatibile con tutti i browser
web che supportano questo tipo di tecnologia.
Essendo
un codice eseguibile il vostro browser potrebbe bloccarlo chiedendovi se
consentirne l�esecuzione.
Il
Software � stato testato con i seguenti Browser Web: Internet Explorer, Google
Chrome, Opera, Safari, e Mozilla con ottimi risultati (c�� qualche piccola
differenza grafica). Sorprendentemente il sistema funziona anche con gli
smartphone di ultima generazione in quanto i browser web caricati dai sistemi
operativi moderni tipo Android, Apple e Windows Mobile, pur essendo sviluppati
con funzioni minime, posseggono il linguaggio Javascript.
La
pagina contiene zone destinate all�immissione dei dati e zone per la
visualizzazione dei risultati; quest�ultime sono disabilitate quindi non sono
soggette all�inserimento accidentale dei dati.
Nel
sottotitolo avete un link agli algoritmi utilizzati: qui troverete tutte le
formule del programma, potrete visualizzare il tipo di sequenza di calcolo che
� stata sviluppata e quali algoritmi sono presenti all�interno del sistema.
Prima
di inserire i valori nei campi, almeno per le prime volte, � utile cliccare sui
pulsanti �?� questi aprono una finestra che spiega in che modo vanno inseriti i
valori.
E�
importante che inseriate nei campi solo numeri positivi e separiate i decimali
con il punto; per i dati negativi avete a disposizione i pulsanti per il cambio
del segno.
Nella
prima parte della schermata, dopo aver compilato i campi �Sito� e �Note�
secondo le vostre esigenze, dovrete inserire i dati relativi all�orario di
osservazione, alla posizione geografica del sito e all�azimut misurato; a
questo proposito � presente un piccolo programma interno per convertire i gradi
quattrocentesimali, utilizzati dagli strumenti topografici pi� comuni, in gradi
sessagesimali necessari per il calcolo (Pulsante �Converti�). I pulsanti con i
punti interrogativi spiegano nel dettaglio i valori da inserire.
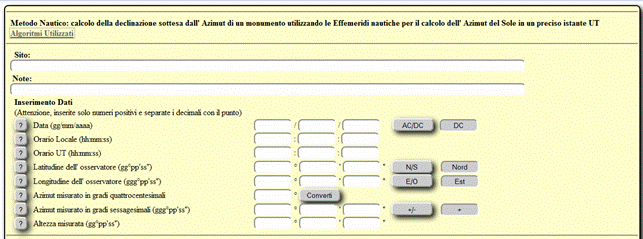
La
seconda parte di inserimento � relativa ai dati necessari, in funzione
dell�orario UT di osservazione, reperibili nelle Effemeridi Nautiche
dell�I.I.M.. I pulsanti con i punti interrogativi spiegano nel dettaglio i
valori da estrarre dal libro delle Effemeridi.

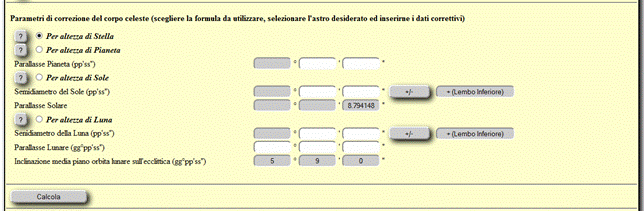
La
terza e quarta parte degli inserimenti � dedicata alla scelta delle formule da
utilizzare per il calcolo dell�altezza vera dell�astro, ai parametri di
correzione per la quota e rifrazione media[26] ed
infine alla scelta del corpo celeste.
Una
volta inseriti tutti i dati cliccate sul pulsante �Calcola� per ottenere i
risultati: azimut del Sole, azimut dell�allineamento, declinazione sottesa
dall�allineamento e declinazione sottesa dall�allineamento opposto ovvero (reciproco).
In questo programma avete la possibilit�, dopo aver premuto il pulsante
�Calcola�, di utilizzare anche i pulsanti sottostanti di cui fornisco ora una
breve descrizione:
�Tabella
Risultati� : questo pulsante visualizza una pagina web contenente tutti i
risultati degli algoritmi che il programma esegue al suo interno; il link
�Stampa� funziona solamente se il Vostro PC � collegato ad una stampante ed il
link �Esporta in Excel� funziona solo se utilizzate il browser Internet
Explorer, in quanto il comando di esportazione non � riconosciuto dagli altri
browser; ad ogni modo potete comunque selezionare tutta la pagina e copiarla in
un qualunque elaboratore di testi tipo Word.
�Lista
Risultati�: questo pulsante visualizza una pagina web contenente tutti i
risultati degli algoritmi che il programma esegue al suo interno ma questa
volta, a differenza di �Tabella Risultati�, la formattazione della tabella �
molto pi� spartana della precedente (in formato testo) e consente quindi il
copia/incolla dei dati anche su un comune Notepad di Windows.
�Esporta�:
questo pulsante funziona solo se il programma � stato scaricato e decompresso
sul vostro Hard Disk e solo se si utilizza il browser Internet Explorer, il
pulsante creer� il file �dati_calcolo_nautico.txt� nell�Hard Disk C:\.
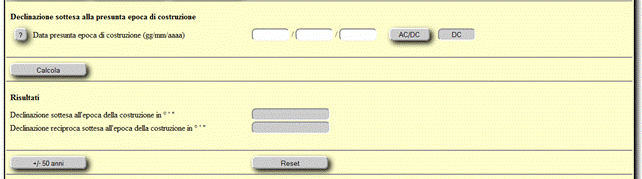
Dopo
aver visualizzato i risultati delle declinazioni sottese dall�allineamento e
riferite alla data di osservazione, avete a disposizione un ulteriore programma
che calcola le declinazioni sottese dall�allineamento riferite ad un�epoca di
nota o stimata costruzione del monumento: inserite la data e cliccate sul
pulsante �Calcola�.
In
seguito sar� possibile anche visualizzare le variazioni di declinazioni di
Il
pulsante �Reset� azzera tutti i campi, risultati compresi.
Gli
algoritmi utilizzati dal programma sono i seguenti:
Calcolo del tempo vero del
Sole
Con i dati inseriti presi
dalle Effemeridi Tv, Iv e parti proporzionali (ν) il
programma calcola il tempo vero locale tv
del Sole
Tv = Tv + Iv � (ν)
tv = Tv � longitudine
Se tv > 180� si sottrae da
360�
Calcolo della declinazione
del Sole
Con i dati inseriti presi
dalle Effemeridi di δ e pp il programma calcola la declinazione
solare δ� vera.
Le parti proporzionali (d) sono interpolate tra il minuto di UT
in corso e quello successivo a seconda dei secondi di UT inseriti; allo scopo
viene utilizzata la seguente formula:
Δpp = pp minuto UT successivo �
pp minuto UT in corso
pp interpolate = Δpp * secondi di UT / 60 + pp minuti UT in corso
le parti proporzionali
vengono poi trasformate in gradi decimali:
pp(�dec) = pp interpolate /
60
δ vera = δ � pp (�dec)
Calcolo dell�altezza e
dell�azimut del Sole
Altezza del Sole
h = arcsen (sen φ * sen δ
+ cos φ * cos δ * cos tv)
Azimut del Sole
cos
A = (sen δ � sen φ * sen h) / (cos φ * cos h)
Calcolo azimut
dell�allineamento del monumento
Aa = A + (� azimut misurato)
Calcolo della correzione
delle altezze vere di stella, pianeta, Sole e Luna
(ho = altezza osservata; Q =
quota media sul livello del mare + altezza dal suolo dell�occhio
dell�osservatore[27]; R = rifrazione
atmosferica media; P = parallasse[28]; Sd
= semidiametro del Sole o della Luna; φ = latitudine dell�osservatore)
Formule semplificate[29]:
Altezza vera di stella
hv = ho � 0,03 * (√Q) � R
Altezza vera di pianeta
hv = ho � 0,03 * (√Q) � R + (P * cos ho)
Altezza vera di Sole o Luna
hv = ho � 0,03 * (√Q) � R � Sd + (P * cos ho)
Formule Nautiche
Altezza vera di stella
hv = ho � 0,03 * (√Q) � R
Altezza vera di pianeta
hv = ho � 0,03 * (√Q) � R + arcsen {sen [P � P *
(1 � 298,257) * (sen φ)�] * cos (ho � 0,03 * (√Q) � R)}
Altezza vera di Sole o Luna
hv = ho � 0,03 * (√Q) � R � Sd � [1 + sen (ho �
0,03 * (√Q) � R) * sen P] + arcsen {sen [P � P * (1 / 298,257) * (sen φ)�] * cos (ho � 0,03 * (√Q) * R)}
Formule Geodetiche
Altezza vera di stella
hv = ho � 0,03 * (√Q) � R
Altezza vera di pianeta
hv = ho � 0,03 * (√Q) � R + arcsen {[0,9983271 +
0,0016764 * cos (2 * φ) � 0,0000035 * cos (4 * φ)] * sen P * cos (ho
� 0,03 * (√Q) � R)}
Altezza vera di Sole o Luna
hv = ho � 0,03 * (√Q) � R � Sd � {1 + sen [ho �
0,03 * (√Q) � R] * sen P} + arcsen {[0,9983271 + 0,0016764 * cos (2 * φ) � 0,0000035 * cos (4 * φ)] * sen P * cos (ho � 0,03 * (√Q) � R)}
Calcolo della declinazione
sottesa dall�allineamento misurato all'epoca attuale
δa = arcsen (sen φ * sen hv + cos φ * cos hv * cos Aa)
Calcolo
della declinazione sottesa dall�allineamento misurato all�epoca di presunta
costruzione del monumento
Per
questo calcolo il programma calcola il numero di secoli giuliani intercorsi tra
l�epoca di presunta costruzione del monumento e l�epoca standard J2000 pari a
JD2451545,0 ottenendo quindi il parametro di calcolo T1 con la seguente
formula:
T1 = (JD Epoca � 2451545,0) / 36525
Dopodich�
il programma calcola la declinazione sottesa dall�allineamento del monumento
risultante all�epoca di presunta costruzione dello stesso tenendo in
considerazione l�obliquit� dell�eclittica ottenuta con la formula di Laskar:
δa1 = δa � 1�18�00,93� * (U) � 0�00�01,55� * (U)� +
0�33�19,25� * (U)� � 0�00�51,38� + (U)4 � 0�04�09,67� * (U)5
� 0�00�39,05� * (U)6 + 0�00�07,12� * (U)7 + 0�00�27,87� *
(U)8 + 0�00�05,79� * (U)9 + 0�00�02,45� * (U)10
(dove
U = T1/100).
Per
qualsiasi dubbio, domande, segnalazioni di errori ortografici e/o di calcolo
non esitate a contattarmi ago.pax@libero.it
. Il Programma � volutamente messo a disposizione gratuitamente per poter essere
testato dal maggior numero possibile di persone.
BIBLIOGRAFIA
�
AA.VV.
(1976-1987). Enciclopedia delle
matematiche elementari e complementi, Hoepli, Milano.
- Codeb� Mario (1997).
Problemi generali del rilevamento
archeoastronomico, Atti I Seminario A.L.S.S.A., Genova.
�
Codeb� Mario
(1997a). Prime indagini
archeoastronomiche in Liguria, memorie S.A.It. 68, n. 3.
�
Codeb� Mario
(2010). L�algoritmo giuliano del Sole,
Atti XII Seminario A.L.S.S.A., Genova.
- Codeb� Mario (2011). Il calcolo FK4 B1950.0 della
precessione delle stelle,
Atti XIII Seminario A.L.S.S.A., Genova.
- Codeb� Mario (2012). Il calcolo FK4 B1900.0
della precessione delle stelle, Atti XIV Seminario A.L.S.S.A., Genova.
�
Flora Ferdinando
(1987). Astronomia nautica, Hoepli,
Milano.
- Lenzi Ernesto.
(1967). Determinazioni astronomiche
speditive, I.G.M., Firenze.
- Meeus Jean (1988). Astronomical
formulae for calculators, Willmann-Bell Inc., Richmond, Virginia, U.S.A..
- Meeus Jean (1990). Astronomia con il computer, Hoepli,
Milano.
�
Meeus Jean (1998). Astronomical
algorithms, Willmann-Bell Inc., Richmond, Virginia, U.S.A..
�
Meeus Jean (2005) Astronomical
algorithms, 2nd edition, Willmann-Bell Inc., Richmond, Virginia, U.S.A.
�
Smart William Marshall. (1977). Textbook on Spherical Astronomy, Cambridge University Press,
Cambridge, U.K..
�
Tavole Nautiche.
I.I.M., Genova, 1961.
�
Zagar Francesco
(1984). Astronomia sferica e teorica,
Zanichelli, Bologna.