ARCHAEOASTRONOMICAL SURVEYS IN VILLA ADRIANA OF TIVOLI

This report was written at the beginning as an appendix of a book, therefore it was longer and more detailed; but, owing to the lack of agreement with the other joint authors, it is now edited like a single report. Moreover, owing to restrictions on printing space, we are obliged to remove the detailed description of calculation routines and algorithms and to describe only the results of our archaeoastronomical surveys in Roccabruna, Apollo’s Temple, Pecile, Marine Theatre, Imperial Palace and Three Exedras Building of Villa Adriana in Tivoli (Rome), using a spherical graduated surveyor’s cross and an inclinometer^{^[1]}and also using a photo taken by Giuseppe Veneziano at Apollo’s Temple on 21 October 2010 Greenwich Universal Time Tm 18h 03m^{^[2]}. All the procedures and calculations^{^[3]} were published in Codebò & Salvo 2011 and they will be published on the web dominion http://www.archaeoastronomy.it.[4]

1) Roccabruna, φ 41°56’16.63”N; λ 12°46’23.13”E; m. 110 above sea level (Google Earth coordinates by G. Veneziano)^{^[5]}

1.1) 2010 A.D. aequinoctial and solstitial Sunrises and Sunsets parameters (chart No 1):

Time	sunrise azimuths	sunset azimuths	sunrise astronomical time tv	sunset astronomical time tv
Spring Aequinox	90°	270°	6h	18h
Summer Solstice	57°40’30.21”	302°19’29.79”	4h 28m 18.3s	19h 31m 41.7s
Autumnal Aequinox	90°	270°	6h	18h
Winter Solstice	122°19’29.79”	237°40’30.21”	7h 31m 41.7s	16h 28m 18.3s

1.2) 125 A.D.^{^[6]} aequinoctial and solstitial Sunrises and Sunsets local parameters (chart No 2):

Time	sunrise azimuths	sunset azimuth	sunrise astronomical time tv	sunset astronomical time tv
Spring aequinox	90°	270°	6h	18h
Summer solstice	57°19’22.48”	302°40’45.65”	4h 27m 11.08s	19h 32m 48.92s
Autumn aequinox	90°	270°	6h	18h
Winter solstice	122°40’37.52”	237°19’22.48”	7h 32m 48.92s	16h 27m 11.08s

1.3) 125 A.D. summer solstice sunset probable local astronomical (or: true) standard time: 19h 39m;

1.4) 125 A.D. summer solstice sunset probable local mean standard time: 19h 46m.

Italian summer time is one hour more.

The calculations 1.4) and 1.5) cannot be sure because of the uncertainty of the Time Equation ET calculated by Smart formulas^{^[7]}.

1.5) Our instrumental^{^[8]}survey on 01 October 2010, Local Mean Time tm 12h 40m 05s, φ GPS^{^[9]} 41°56’17”N, λ GPS 12°46’23”E, m. GPS 103 above sea level, Instrumental Height of the horizon^{^[10]} hi –1°30’, Instrumental Azimuth Ai 59.2g = 53°16’48”, Compass Azimuth Ac 302°30’^{^[11]}, gave us the Astronomical Azimuth Aa 300°12’52.8”

This is the same azimuth of the summer solstitial sunset minus 2°. Therefore, Roccabruna axis differs from the summer solstitial sunset azimuth about 2° only. A setting in a row towards the summer solstitial sunrise azimuth does not exist because this direction is obstructed by a large niche on which Sun rays are cast. The duct B above Roccabruna’s entrance has exactly the same orientation, therefore it has no astronomical role. Probably it has an architectural role (like all other ducts).

2) Apollo’s Temple φ 41°56’12.32”N; λ 12°46’39.56”E; m. 114 above sea level (Google Earth coordinates by G. Veneziano)

2.1) 2010 A.D. aequinoctial and solstitial Sunrises and Sunsets parameters (chart No 3):

Time	sunrise azimuth	sunset azimuth	sunrise astronomical time tv	sunset astronomical time tv
Spring aequinox	90°	270°	6h	18h
Summer solstice	57°40’32.66”	302°19’27.34”	4h 28m 18.54s	19h 31m 41.46s
Autumn aequinox	90°	270°	6h	18h
Winter solstice	122°19’27.34”	237°40’32.66”	7h 31m 41.46s	16h 28m 18.54s

Then we calculated, according to Apollo’s temple coordinates:

2.2.1) the Local Mean Time of the astronomical sunset: tm 20h 42m 23.71s;

2.2.2) the Time Equation ET^{^[12]}, but inverting the mathematical symbols + and – to get the True Time Equation ETv = Tm – Tv^{^[13]}, not the Mean Time Equation ETm = Tv – Tm. This ETv, on 21st June 2010 tm 20h 03m was: +0h 01m 48.87s (1m 46s at noon and 1m 53s at midnight according to Italian Nautical Almanac I.I.M.);

2.2.3) we turned the Instrumental Height hi 0°00’00” into True Height hv -1°11’15.33”;

2.2.4) we calculated the ΔPm^{^[14]}: 0h 07m 31.23s;

2.2.5) we calculated the Apparent sunset Mean Time^{^[15]}: 20h 49m 57.13s;

2.2.6) finally, we could calculate the Sun’s azimuth in the exact moment – 21^st June 2010, Tm 18h 03m – in which Veneziano photographed the Sun in the upper left angle of the Apollo’s Temple northern door: 295°56’21.45”;

2.2.7) we calculated also height h and time tm of the True and Apparent sunset in the lower right angle of the same door, i.e. at its sunset, solving the spherical oblique triangle of which we knew two sides – the Polar Distance and the Colatitude – and the angle not included, i. e. the azimuth (we calculated the azimuth using the simple plane trigonometry formula tan β = b/c and adding the result to 295°56’21.45”)^{^[16]}: h 0°05’41” and True sunset tm 19h 32m 55.31s (20h 32m 55.31s summer time). The time of the local True sunset was transformed in time of local Apparent sunset adding ΔPm and ETv to the local True sunset Mean Time: 20h 49m 23.54s.

Time 2.2.5) 20h 49m 57.13s is very similar to time 2.2.7) 20h 49m 23.59s.

2.3) Two instrumental surveys on 02^nd October 2010 – φ GPS 41°56’12”N, λ GPS 12°46’40”E, m. GPS 119 above sea level, ho unknown because some trees obstructed the view of the horizon, Ai 18,5g = 16°39’, Ac 295° – gave us the next astronomical azimuths Aa:

2.3.1) Local Mean Time tm 10h 42m 13s: Aa 300°22’57.12”;

2.3.2) Local Mean Time tm 10h 44m 45s: Aa 300°03’58.03”;

Therefore, the mean astronomical azimuth Aam was 300°13’27.57” σ ± 0.16. This azimuth is equivalent to the axis passing through the centre of Apollo’s Temple door and its inverse 120°13’27.57” is equivalent to the one passing through the centre of the door which is diametrically opposed and allowed the entrance into the so called Zooteca ( = animals room). This inverse azimuth is a good approximation, at less than 2°, of the local sunrise winter solstitial azimuth 122°19’27.34”. Moreover, Elena Salvo and Giuseppe Veneziano personally saw the sunrise in that direction on winter solstice in 2009.

We can deduce, both from the picture taken on 21^th June 2010 and from the measurements of 2^nd October 2010, that the axis of Apollo’s Temple doors are on the solstitial axis at less than 2° and that, therefore, the rise and the setting of the Sun on solstices is visible set in their frame.

It is evident that the axes of the doors of Roccabruna and of Apollo’s Temple have almost the same azimuth: 300°12’52.8” the first one and 300°13’27.57” the second one (the difference is 34.77”!) and that these two azimuths have a difference of 2° from the local summer solstitial sunset 302°19’. Therefore, when the Sun is exactly on the axis of the doors (its height is 2°01’^{^[17]} at that time) must cover 2° more to set on the horizon: we think that this difference between the axes azimuths and the local summer solstitial sunset is not random but wilful: the builders wanted the Sun to go through the whole frame of the door before setting at the lower right angle of the door.

3) The Roccabruna’s ducts A, B, C, D, E

Ducts A, B, C and the common outlet of ducts D and E, have the same azimuths of the axes of Roccabruna: 300°12’52.8” ↔ 120°12’52.8” and 30°12’52.8” ↔ 210°12’52.8”. As we wrote above, the duct B direction 120°12’52.8” is obstructed by a large niche (in which there is the common outlet of the ducts D and E); the duct C direction 30°12’52.8” is astronomically meaningless (with regard to Sun and Moon); the duct A direction 210°12’52.8” is reached by the Sun every day in the year, therefore it is astronomically meaningless too (just because it has all astronomical meanings!). In the chart No 4 there are height and time transit of the Sun at the azimuth of duct A[18]. Clearly, time transits in all other days of a year are between the summer and the winter solstices time transits:

Time	Sun height	Tm[19] transit	Tm[20] transit
Spring aequinox	44°17.3’	13h 40m 00s	12h 40m 00s
Summer solstice	69°19.3’	12h 55m 04s	11h 55m 04s
Autumn aequinox	43°47.3’	13h 25m 56s	12h 25m 56s
Winter solstice	18°34.7’	14h 11m 53s	13h 11m 53s

The duct B has the same direction of Roccabruna’s door toward the local summer solstitial sunset. The azimuth of duct D is 84°30’42.91” and the height of the horizon in this direction is 8.5°; therefore the subtended declination is 9°16’58.27”; the azimuth of duct E is 155°01’08.43” and the height of the horizon in this direction is 1.5°, therefore the subtended declination is -41°: no astronomical meaning can be given to all the ducts! We can conclude that the Roccabruna ducts function surely was not astronomical; maybe it was architectural[21].

4) The so called Miraglio

It is a duct in the west wall of Roccabruna. It is m. 1.956 from the ground; m. 6 long, m. 0.57 large, m. 0.61 height; its inclination is 15° – 16° and its azimuth is 210°. For a person standing whose eyes are at m. 1.68 from the ground, its inclination is between a minimum of 19° and a maximum of 26°, that is less than 30° used by Castellani^{^[22]}. For this reason we can state that the area of the sky framed by its opening is between the declinations δ –23° and δ –16.5°. Taking into account an average inclination of 22.5°, we obtain a declination δ –19.8°, considering a person at m. 1.68 from the ground. These results show us that the area of the sky between Aquila, Sagittarius, Scutum and Capricornus constellations – i.e. the area in which the old constellation, or better the star, of Antinoo was – is now, and used to be in Hadrian’s time, visible in summer and in spring, while in other seasons or at nightime other constellations are and were visible. Therefore we think that it is important to link this phenomenon with some meaningful dates in Antinoo’s life and the only one we know is the date of its death: the 30th October 130 A.D. We verified what happened on that occasion using the astronomical softwares Cybersky and Planetario 2.0[23]: Antinoo’s star or constellation crossed the azimuth 210° of the Miraglio at 5 p.m. local time – at about a quarter to 5 p.m. in 130 A.D. – i.e. at sunset time. Therefore, at the beginning of the twilight (picture No 1), as in this area there are only low magnitude stars difficult to be seen with a naked eye, these stars could have been noticed only at the end of astronomical twilight^{^[24]}, when that portion of the sky was already out of the opening frame (picture No 2).

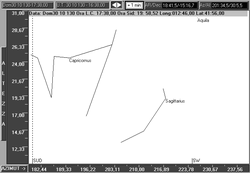
Picture No1[25]

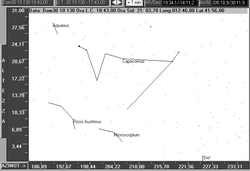
Picture No 2[26]

5) The Pecile

East end: φ 41°56’32.18”E; λ 12°46’30.80”W; m. 95 (Google Earth coordinates);

West end: φ 41°56’32.62”N; λ 12°46’22.32”E; m. 95 (Google Earth coordinates);

Using four measurements, its average astronomical azimuth is 273°48’50.95” ↔ 93°48’50.95” σ ± 0.2444. Its hv is 0°25’ westward and 9°30’ eastward. Pecile’s subtended declinations are consequently in 2011: 3°06’53.75” westward and 3°17’39.76” eastward. In 125 A.D. they were 3°21’18.07” westward and 3°32’04.08” eastward. Therefore, it is not oriented E – W exactly but plus 3.5° clockwise. But these 125 A.D declinations are the ones that the Sun has in March 29 and in September 14 – 13. Therefore, considering that the spring aequinox date in the Julian calendar was March 25th^{^[27]}, we can conclude that the Pecile was oriented according to what the Romans believed to be the aequinoctial line^{^[28]}.

6) The Marine Theatre (Teatro Marittimo)

φ 41°56’33”N; λ 12°46’33”E; m. 95 (GPS coordinates).

By means of five measurements, we got an average azimuth 162°24’09.37” ↔ 342°24’09.37” σ ± 0.2576. We could not measure the horizon height – and it has no meaning! – because the Marine Theatre is surrounded by a very high wall which blocks view all around: therefore, any astronomical hypothesis is meaningless.

7) The Imperial Palace

φ 41°56’31.68”N; λ 12°46’37.53”E; m. 101^{^[29]} (Google Earth coordinates)

Its average azimuths (two measurements) are: 273°02’13.65” ↔ 93°02’13.65” σ ± 0.251 and the heights of the horizon are 1°30’ westward and 9°30’ eastward. The subtended declinations are: 2°24’26.45” in 2011 and 2°38’50.77” in 125 A.D. westward; 3°40’10.22” in 2011 and 3°54’34.54” in 125 A.D. eastward. The Sun has declination 2.5° on March 27^th and on September 16^th and declination 3.8° on March 30^th and on September 13^th respectively. We can conclude that the Imperial Palace was oriented like the Pecile.

8) The Building with Three Exedras

We got five measurements. Its average azimuths are 1°51’20.82” ↔ 181°51’20.82” σ ± 0.423: it lies along the meridian line with an error less than 2° clockwise. Consequently, its azimuths westward and eastwards are 271.9° ↔ 91.9°: it is oriented like Pecile and Imperial Palace, but with a bit more accuracy regarding to the true aequinoctial line and with a little bit less accuracy regarding what the Romans thought was the aequinoctial line.

9) The magnetical declination

During our surveys in 2010 we measured the magnetical declination on the spot (chart No 4):

Place	Astronomical azimuth	Magnetical azimuth	Difference^{^[30]}
Roccabruna	300°12’52,8”	302°30’	–2°17’07,2”
Apollo’s Temple	300°13’27,57”	295°	5°13’27,57”
Duct D	84°30’42,91”	81°	3°30’42,91”
Duct E	155°01’08,43”	156°	–0°58’51,57”

As the readers can see, the magnetical declination, which should be 2°30’ East according to Magnetical Map of Italy I.G.M., is very variable: at Roccabruna and at duct E it is western while in Apollo’s Temple and in duct D is eastern, but with an higher absolute value. We can deduce that in Villa Adriana there are several magnetical anomalies and compass surveys are not trustworthy.

10) Conclusions

Roccabruna and Apollo’s Temple are clearly oriented toward the skyline solstitial points. The ducts A, B, C, D, E are astronomically meaningless. This is probably the case of Miraglio too, even though it is directed toward the heavenly position of Antinoo’s constellation or star. The Pecile, the Imperial Palace and the Building with Three Exedras are oriented toward the position of the local sunset spring aequinox according to its date in the Julian calendar: March 25. The Marine Theatre has no astronomical setting in a row. The rest of the buildings of Villa Adriana were not measured yet, but we must remember that Villa Adriana hasn’t had any historical layers which lasted for centuries (like, for instance, the Roman Forum), but it is the building of a single Roman emperor, it was built by him and it was forsaken after his death. Therefore we cannot expect great astronomical outcomes.

Acknowledgments

We thanks sincerely Stefania della Scala for her great contribution to the English version of this our report. We are grateful to everyone supporting us in these researches.

Bibliographical references

· AA.VV. (2005). Carta magnetica d’Italia, I.G.M., Firenze, Italy.

· AA.VV. (2009). Effemeridi Nautiche, I.I.M., Genova,Italy.

· AA.VV. (2010). Effemeridi Nautiche, I.I.M., Genova, Italy.

· Cappelli A. (1998). Cronologia, cronografia e calendario perpetuo, Hoepli, Milano, Italy.

· Castellani V. (2006). Tivoli: Villa Adriana, Roccabruna e Astronomia, Rivista Italiana di Archeoastronomia, IV.

· Chiesa A. &.R. (2004). Punto nave facile col computer, Incontri Nautici, Roma, Italy.

· Cinque G. E. - Lazzeri E. (2010). Roccabruna: un’architettura adrianea a immagine del cielo, in: Mensura Caeli, Proceedings of 8th National Meeting of Società Italiana di Archeoastronomia S.I.A., UnifePress, Ferrara, Italy.

· Codebò M. (1997a). Uso della bussola in archeoastronomia. Proceedings of Astronomy and Physics History 16th National Meeting C.N.R., Milano, Italy.

· Codebò M. (1997b). Problemi generali dell’indagine archeoastronomica, Proceedings of 1st A.L.S.S.A. Archaeoastronomy Workshop, Genova, Italy.

· Codebò M. (2010). L’algoritmo giuliano del Sole, Proceedings of 12th A.L.S.S.A. Archaeoastronomy Workshop, Genova, Italy.

· Codebò M. - Salvo E. (2011). Orientamenti astronomici di Roccabruna e Tempio di Apollo: algoritmi e calcoli, Proceeding of A.L.S.S.A. 13rd Archaeoastronomical Workshop, Genova, Italy.

· Flora F. (1987⁵). Astronomia Nautica, Hoepli, Milano, Italy.

· Maddalena E. (1988). Orienteering, Hoepli, Milano, Italy.

· Meeus J. (1988⁴). Astronomical Formulae for Calculators, Willmann-Bell Inc., Richmond, Virginia, U.S.A.

· Meeus J. (1990). Astronomia con il computer, Hoepli, Milano, Italy.

· Meeus J. (2005). Astronomical Algorithms, Willmann-Bell inc., Richmond, Virginia, U.S.A.

· Pannunzio R. (2002). Moti della Terra e scale di tempo nell’astronomia moderna, Internal Report dO.A.To., Pino Torinese (TO), Italy.

· Pesci G. (1911). Trigonometria piana e sferica, Raffaello Giunti editore, Livorno, Italy.

· Smart W. M. (1977⁶). Textbook on Spherical Astronomy, Cambridge University Press, Cambridge, U.K.

· Zagar F. (1984). Astronomia sferica e teorica, Zanichelli, Bologna, Italy.

Torna all’indice cronologico.

Torna all’indice tematico.

Torna alla pagina iniziale.

[1] The zenith measures were obtained using an Abney’s spirit – level (accuracy 0°10’) with tripod, or a Suunto inclinometer (accuracy 1°).

[2] We thank Giuseppe Veneziano for allowing us to use a picture taken by him as well as the data gathered by him.

[3] All the procedures used are taken from the following publications: Codebò 1997; Codebò 2011; Flora 1987⁵; Meeus 1990; Meeus 2005; Pesci 1911; Smart 1977⁶.

[4] Codebò wrote §§ 1 – 4; Salvo wrote §§ 5 – 9.

[5] All readings are written here with all decimals displayed by the calculator CASIO fx-9700GE for teaching aims. The algorithms we used are now compiled in JavaScript by Agostino Frosini (look at the web site http://www.archaeoastronomy.it); therefore, they work on several PC and Android browsers.

[6] We used the Laskar’s formula (Meeus 2005, pp. 147 – 148) to convert present declinations into ancient declinations.

[7] Smart. 1977⁶, pp. 146 – 150; Meus 1988⁴, pp. 91 – 92; Meeus 1990, pp. 93 – 94.

[8] Instrumental means that the measurement was got using an instrument.

[10] I.e. the height of the horizon measured using the inclinometer or the Abney’s spirit – level

[12] Smart. 1977⁶, pp. 146 – 150; Meus 1988⁴, pp. 91 – 92; Meeus 1990, pp. 93 – 94.

[13] Mean Time Equation ETm is the difference between the True Sun Hour Angle Tv and the Mean Sun Hour Angle Tm. True Time Equation ETv is the difference between the Mean Sun Hour Angle Tm and the True Sun Hour Angle Tv.

[17] Calcolo dell’altezza eseguito con il software Puntonav annesso al libro A & R. Chiesa 2004.

[18] According to the software Puntonav enclosed in Chiesa 2004.

[23] By kindness of Piero Massimino, owner of the software Planetario 2.0.

[28] The true aequinoctial line has azimuths 270°00’00” ↔ 90°00’00” and it subtend the Sun’s declination 0°00’00”. The Su n gets it about on March 21 and September 23.

[29] The Imperial Palace, the Marine Theatre and the Building with Three Exedras are in fact at the same height above the see level: this is a little but irrelevant difference between GPS and Google Earth data.

[30] Magnetical declination east is +; magnetical declination west is – . To calculate “on the spot” the magnetical declination it is compulsory to subtract magnetical azimuths from geographical/astronomical azimuths (Maddalena 1988, pp. 87 – 88; Codebò 1997a, pp. 323 – 335).